MAISY Energy Use and Hourly Loads Databases

Assessing Retail Utility Market Profit Potentials: Pitfalls of Traditional Analysis

This section shows why use of aggregate customer-segment load shapes in headroom, or profitability analysis generates unreliable results

Determining which competitive markets to enter and which customer segments to focus marketing efforts on is one of the most critical strategic decisions facing competitive energy service providers (ESPs). The investment required to enter new geographic markets is substantial; estimation of the difference between current electric rates and the cost of serving customers is conducted as part of a decision process which results in a "go" or "no-go" decision concerning new market activity and strategy refinements. Identifying the most profitable market segments is critical to success in competitive markets.

The traditional approach to estimating headroom or potential profits is to characterize load shapes for some manageable number of customer segments, apply these load shapes to the ESP's cost-of-service data and current electric rate structures and subtract other costs including metering, billing, marketing and other overhead functions. If sufficient headroom exists, the utility service area or market segment represents an attractive new market for ESP activity.

Use of aggregate customer-segment load shapes in headroom, or profitability analysis, almost always generates unreliable results. These problems are an algebraic result of aggregation bias which results from aggregating diverse customer load profiles into larger segments and then applying the segment load profiles to compute revenue and cost of service. To demonstrate this, we developed twelve aggregate customer-segment load shapes from a statistically representative sample of utility customers and apply the segment load shapes to rates and cost-of-service data to replicate the traditional approach. Since we have the customer data, we can also compute actual profits directly for individual customers using the same rates and cost-of-service data and sum the result to get an accurate estimate of total potential profits for the service area. Comparing results from the two approaches reveals shortcomings of traditional headroom analysis.*

The commercial sector of a utility serving approximately one million customers is used for this analysis. Data for these customers is drawn from the MAISY Utility Customer DatabAse. In this analysis we assume that the ESP considering this utility service area as a new market has a cost-of-service comparable to the existing utility (the same results will occur with other plausible cost-of-service data).

The chart below shows the results of applying the twelve aggregate customer-segment load shapes to utility rate structures and cost of service using the traditional approach. Customer size was not used to define segments because most of the customers in this utility fall into a single size-defined rate. Total potential profits based on the customer-segment profiles are slightly greater than $10 million. Sector-specific profit potentials range from losses of $2.75 million to profits of $4.5 million.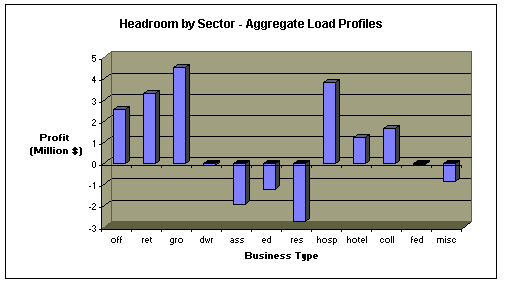

Aggregating across customers to develop the twelve aggregate load profiles and applying rates and cost of service will not ordinarily provide the same results as computing revenue for individual customers.* However, if intra-segment customer variability is small compared to variability across segments, the level of aggregation bias may be insignificant. The chart below presenting aggregate results along with the true individual customer calculations shows that aggregation bias is, in fact, quite significant. The true individual customer calculations were developed by computing profit for each of the 1076 customers in the representative sample and summing the profit from these individual customers within business types to get profits based on individual customer loads. Comparing these true profits to the biased profits based on customer segment averages reveals the inaccuracies of using the segment profiles shown in the second chart.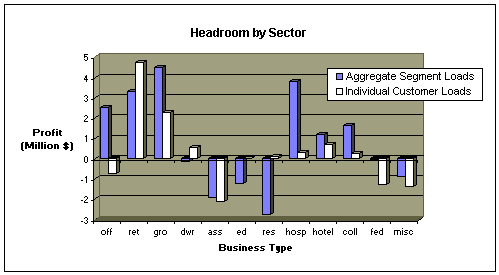

As these results indicate, profitability computations based on aggregate load shapes provide extremely poor estimates for all but one segment (assembly). For offices (off) and warehouses (dwr) sector-specific profit has the wrong sign. These results illustrate the inaccuracy of the segment-specific profitability estimates. Estimation error for eight of the twelve segments is greater than 90 percent.

Summing profit for individual customers across sectors reveals a true total profit potential of $3.5 million. However, segment-wide results reflect the sum of profits, some positive and some negative, across customers within each segment. Evaluation of the individual customer profit data shows that the $3.5 million in profit for the entire commercial sector actually reflects $22 million in profit and $18.5 million in losses for a net profit of $3.5 million. The chart below shows profits for each customer quintile where customers have been sorted from least profitable to most profitable. If the ESP coming into the service area gets the same ratio of profitable to unprofitable customers as the utility currently has, the profit potential is $3.5 million. If the ESP were able to avoid the one-fifth of all customers who are unprofitable, the profit potential is $22 million. Thus the headroom or profit potential for commercial customers in the service area is more accurately characterized as between $3.5 and $22 million; the profit potential actually achieved will depend on the the ESP's ability to identify, target and win profitable customers in the service area.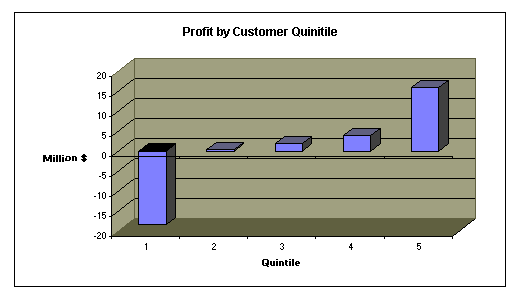

In summary, this analysis used a sample of utility customers to demonstrate the unreliable nature of traditional "headroom" or profitability analysis applied to evaluate utility markets and submarkets. These results are an unavoidable consequence of aggregation error which cannot be mitigated except by dramatically increasing the number of customer segments or by using the kind of individual customer data available in the MAISY Utility Customer Databases.

The extent of the segment-based headroom error identified in this analysis is a function of the nonlinearity in rate structures and cost of service and the diversity of customer energy and demand characteristics. The service area used in this analysis represents a minimum of rate-structure and cost of service nonlinearity and a modest level of customer diversity. Consequently, these results should be viewed as reflecting the least biased outcome that can be expected using segment-average load shapes.

* Aggregation bias, in this instance, is a result of the fact that customer revenue and cost of service are both nonlinear functions of hourly loads. With nonlinear functions the value derived from an average input is different than the average of the values derived from the individual inputs. For example consider the function y = x². With x values of 2, 4 and 10, we get an average x value of 5.33 which evaluates to 28.4 (i.e., 5.33²). Evaluating each of the values individually provides three y values, 4, 16 and 100 whose average is 40.0. The aggregation bias in this example is 29% ( (40-28.4)/40 ). The true profit or headroom figure is determined by the profit provided by each customer; consequently, any discrepancy between the results based on aggregate load profiles and the results based on individual customer calculations reflects aggregation bias.